Основы вакуумной техники

И.В.БЕЛОКРЫЛОВ

Конспект лекций

3.Физические процессы в вакууме

3.1. Вязкость газов

При перемещении твердого тела со скоростью vnза счет передачи количества движения молекулам газа возникает сила внутреннего трения.
Сила трения по всей поверхности переноса, согласно второму закону Ньютона, определяется общим изменением количества движения в единицу времени:

,                (3.1)

где А– площадь поверхности переноса; η – коэффициент динамической вязкости.

 

.                                     (3.2)

С учетом законов распределения молекул по скоростям и длине свободного пути
                                             (3.3)

Подставляя коэффициенты η и L, зависящие от давления, получаем

 ,                                           (3.4)

т. е. динамическая вязкость не зависит от давления при низком вакууме.
Температурную зависимость коэффициента вязкости можно определить по формуле
                                        (3.5)

Т. е. η зависит от ТХ, где х=1/2 – при высоких температурах (T>>C) и х=3/2 – при низких температурах (T<<C).
В области высокого вакуума силу трения можно рассчитать по уравнению

                               (3.6)

Т. е. сила трения в области высокого вакуума пропорциональна молекулярной концентрации или давлению. Данное уравнение можно преобразовать к виду
                             (3.7)

В области среднего вакуума можно записать аппроксимирующее выражение

.                                         (3.8)

Здесь d – расстояние между поверхностями переноса.
Вязкость газов используются для измерения давления в области среднего и высокого вакуума. Однако вязкостные вакуумметры не получили широкого распространения из-за длительности регистрации давления. Гораздо шире вязкость газов используется в технике получения вакуума. На этом принципе работают струйные, эжекторные насосы для получения низкого вакуума.

3.2. Перенос теплоты в вакууме

Теплопередача в разреженных газах может происходить за счет конвекции, теплопроводности и излучения.
При низком вакууме конвективный теплообмен играет важную роль. Перенос теплоты конвекцией от поверхности нити, нагретой до температуры Тм, к стенкам вакуумной камеры, имеющим температуру Т, описывается уравнением

,                                   (3.9)

где α — коэффициент теплообмена; А — площадь поверхности нити. При свободной конвекции из-за силового воздействия гравитационного поля на газ, имеющий различную плотность вследствие температурных градиентов, коэффициент теплообмена
                                  (3.10)

где: а — экспериментальный коэффициент, зависящий от материала и формы поверхности.
Коэффициент теплообмена в условиях вынужденной конвекции при поперечном обтекании нити для воздуха
 ,                                   (3.11)

где λ — коэффициент теплопроводности газа; d— характерный размер (диаметр нити);  — критерий Нуссельта;Re — критерий Рейнольдса; k1и k2— константы, зависящие от числа Re: k1=0,45; k2=0,5 при Re<103 и k1=0,245; k2=0,6 при Re>103.
Теплопроводность газа в качестве явления переноса при низком вакууме можно рассматривать аналогично вязкости газа. Вместо количества движения в этом случае переносится энергия молекул газа. Количество теплоты, отнесенное к одной молекуле газа
,(3.12)

где: cv— теплоемкость газа при постоянном объеме; m— масса молекулы газа;      Т — абсолютная температура.
Если концентрация газа п постоянна, то аналогично можно записать выражение для теплового потока:
,(3.13)
где λН — коэффициент теплопроводности газа при низком вакууме:
                        (3.14)

Таким образом, коэффициент теплопроводности газа равен произведению коэффициента динамической вязкости на удельную теплоемкость газа при постоянном объеме. Для расчета cvможно использовать выражение

,                                   (3.15)

где:— отношение теплоемкости газа при постоянном давлении к теплоемкости при постоянном объеме (для одноатомных газов γ= 1,66; для двухатомных γ =1,4; для трехатомных γ =1,3); k— постоянная Больцмана;    m — масса молекулы газа.
Молекулярно - кинетическая теория, используя функции распределения скоростей и длин свободного пути молекул газа, дает для коэффициента теплопроводности более точное выражение
                                   (3.16)

отличающееся не более чем на 20 % от значения, получаемого выражением (3.15).
Характер зависимости коэффициента теплопроводности и коэффициента динамической вязкости газа при низком вакууме от температуры и давления идентичен.
Теплопередачу излучением в низком вакууме можно определить по закону Стефана - Больцмана:
,                          (3.17)

где Еи — плотность теплового потока, Вт/м2; Т1 Т2— температуры на внешней и внутренней поверхности переноса; Ег — геометрический фактор (для параллельных плоскостей и концентричных цилиндрических оболочек Ег=1); Ее — приведенная степень черноты:
,                         (3.18)

где А1 и А2— площади внешней и внутренней поверхностей переноса; е1 и е2— коэффициенты излучения внешней и внутренней поверхностей.
Для гладких поверхностей в случае нержавеющей стали е = 0,1 при Т=300 К и 0,06 при Т=77 К, а для меди, соответственно, е=0,03 и 0,019.
При установке экранов приведенная степень черноты уменьшается пропорционально количеству установленных экранов N. Если A1=A2; e1=e2=e,то приведенная степень черноты
.                             (3.19)

В высоком вакууме конвективным теплообменом для технических расчетов обычно пренебрегают, считая его малым по сравнению с другими способами теплопередачи. Теплопроводность газа в высоком вакууме между двумя поверхностями с температурой Т2  и Т1, можно записать в виде

                  (3.20)
Преобразовав, получим
,                                 (3.21)

где λВ' — коэффициент теплопроводности газа при высоком вакууме:
,                                     (3.22)
т. е. коэффициент теплопроводности при высоком вакууме пропорционален давлению.
Более точное выражение, полученное в молекулярно-кинетической теории

(3.23)
отличается от (3.22) для двухатомных газов на 20 %.
Если при соударении молекулы газа с поверхностью не происходит полного обмена энергии, т. е. коэффициент аккомодации поверхностей переноса меньше единицы, то уменьшение теплового потока учитывается множителем α/(2—α), где α — коэффициент аккомодации для обеих поверхностей переноса.
Таким образом, окончательное выражение для коэффициента теплопроводности газа в высоком вакууме можно записать в виде

             (3.24)

Теплопередачу излучением в высоком вакууме можно рассчитать.
В области среднего вакуума конвективный теплообмен рассчитывают по формулам (3.17)…(3.19), коэффициент теплопроводности газа может быть приближенно определен по выражению
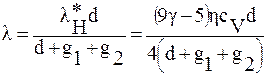,              (3.25)
где
;   .

Здесь а1, а2 — коэффициенты аккомодации поверхностей переноса; L— длина свободного пути при средней температуре.
Для приближенных расчетов можно принять, что Значения а для различных газов и материалов подложки приведены в таблицах. Учитывая, что L=L1/p, преобразуем и получим
,                                 (3.26)

где ;       .

3.3. Скольжение разреженных газов

Экспериментальные исследования течения газа при малых давлениях в магистрали показали, что действительный расход газа больше теоретического, найденного на основании гидродинамических законов ламинарного течения. Это расхождение объясняется тем, что в отличие от ламинарного течения, при котором скорость на поверхности стенки полагают равной нулю, существует скачок скорости, т. е. на поверхности стенки скорость потока газа имеет некоторое значение, отличное от нуля. Такое течение газа называют течением со скольжением. При дальнейшем понижении давления, когда средняя длина свободного пути молекул газа больше расстояния между стенками, молекулы движутся от стенки до стенки практически без межмолекулярных соударений, т. е. наступает свободное молекулярное течение.
При течении со скольжением обычно считают, что градиенты макроскопической скорости и потока газа постоянны и изменяются только непосредственно около поверхности (рис.3.1.) на расстоянии порядка средней длины свободного пути L молекул газа.

Рис. 3.1. Схема течения газа со скольжением.
Для изучения распределения скорости во всем объеме газа на расстояниях, значительно превышающих  L, изменение градиента скорости около поверхности не имеет существенного значения. Для       определения граничных условий движения газа у поверхности достаточно проэкстраполировать линейный участок изменения скорости  до пересечения с поверхностью. Полученное значение uS фиктивной скорости называют скоростью скольжения, причем действительное значение скорости  uS потока у поверхности отличается от значения u1 и от скорости движения поверхности, которая равна нулю, если поверхность неподвижна.
Скорость скольжения вдоль поверхности
,                                                                 

где – градиент скорости газового потока по оси x, перпендикулярной к поверхности стенки; – коэффициент аккомодации тангенциального импульса количества движения; – вязкость газа; – плотность газа; – коэффициент скольжения, имеющий размерность длины:
.
Под коэффициентом скольжения  понимают расстояние, на которое должна быть удалена стенка, чтобы скорость потока на ней, при экстраполяции линейного измерения скорости, равнялась нулю (на неподвижной стенке) или скорости движения стенки.

3.4 Температурный скачок

Явление, аналогичное скольжению, наблюдается и при исследовании теплопроводности разреженных газов, если средняя длина свободного пути L значительно меньше расстояния между поверхностями тел с разной температурой, т. е. существует различие между температурами поверхности TW и газа T1 непосредственно у поверхности.
На расстоянии от поверхности, большем L, градиент температуры в направлении оси x, перпендикулярной к поверхности, остается постоянным и изменяется только около поверхности (рис.3.2.) Отклонение закона изменения температуры около поверхности от линейного объясняется тем, что молекулы отражаются от стенки при некоторой температуре  , отличающейся от температуры стенки TW. Энергия молекул газа, подлетающих к стенке, соответствует температуре слоя газа, в котором они испытали последнее столкновение. При T1 отражении молекул от поверхности температура газа должна быть промежуточной между температурой газа в слое, где молекулы претерпели последние столкновения, и температурой стенки, т. е. действительное значение температуры газа у поверхности T1 отличается и от температуры стенки TW, и от температуры T0, соответствующей линейному изменению температуры поверхности.

Рис. 3.2. Температурный скачок на границе поверхность – газ.

Разность между фиктивной температурой газа T0 у поверхности, определяемой экстраполяцией линейного закона изменения температуры до температуры поверхности, и температурой стенки TW называют температурным скачком:

Здесь – коэффициент температурного скачка, имеющий размерность длины; его представляют как некоторое расстояние, на которое должна быть отодвинута поверхность стенки, чтобы температура газа на ней равнялась температуре стенки при сохранении линейного закона изменения температуры:

,                                 (3.27)

где  – коэффициент аккомодации тангенциального импульса количества движения.
Введя коэффициент аккомодации a, получим

                                  (3.28)

Уравнения (3.27) и (3.28) справедливы для одноатомных газов. Для многоатомных газов

где k– показатель адиабаты; cV– изобарная теплоемкость; λ– теплопроводность.
3.5. Процессы изменения состояния газов вакуумных систем

Во время работы вакуумной системы газ в откаченном объеме расширяется, в результате чего меняется его температура. Непостоянство температуры газа сказывается на точности расчета, что необходимо учитывать, особенно при наличии в системе конденсирующихся паров. В месте с тем, при малых давлениях (меньше 10 Па) процесс расширения газа можно считать изотермическим, так как расширение происходит медленно, и газ успевает воспринимать тепло, от окружающих стенок, сохраняя свою температуру практически постоянной – примерно равной температуре стенок. При изотермических процессах справедлив закон Бойля – Мариотта. При достаточно высоких давлениях в вакуумной системе расширение газа обычно происходит столь быстро, что температура окружающих стенок не успевает сказаться на температуре газа, в таком случае процесс рассчитывается по уравнению адиабаты. Возможны промежуточные политропные процессы.

{jlcomments}